This blog post and the following series captures the path of understanding NLP, usage of Deep Learning in NLP and the various algorithms, by roughly following the lecture patterns for the Cs224n course from Stanford.

Lecture 1 – Introduction and Word Vectors

The following post is primarily about driving home the fact that a word’s meaning can be represented, not perfectly but really rather well by a large vector of real numbers. This has been an amazing find which has taken research away from the traditional approaches followed before deep learning.

Intent

1. foundation - good deep understanding of the effect of modern methods for deep learning applied to NLP.
2. basics & key methods that are used in NLP, recurrent networks, attention transformers
3. Ability to build systems in PyTorch
4. Learning word meanings, dependency parsing, machine translation, question answering.

Language model

1. Building computational systems that try to get better at guessing how their words will affect other people and what other people are meaning by the words that they choose to say.

2. It is a system that was constructed by human beings relatively recently in some sense.

How do word vectors work

Language arose for human beings sort of somewhere in the range of 100,000 to a million years ago. But that powerful communication between human beings quickly set off our ascendancy over other creatures. It was much more recently again that humans developed writing, which allowed knowledge to be communicated across distances of time and space. So a key question for artificial intelligence and human-computer interaction is how to get computers to be able to understand the information conveyed in human languages.

We need knowledge to understand language and people well, but it’s also the case that a lot of that knowledge is contained in language spread out across the books and web pages of the world.

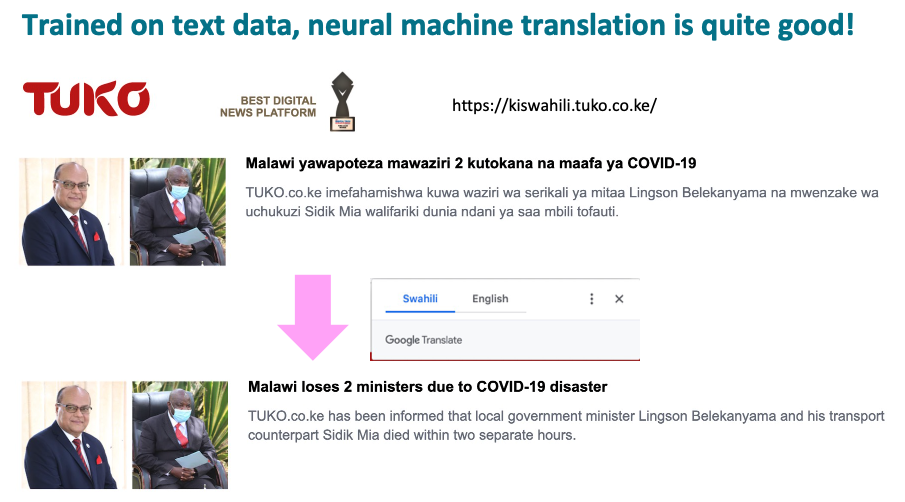
So with recent advancements, machine translation works moderately well. Learning other people’s languages was a human task which required a lot of effort and concentration. But now to get news from Kenya we can use Google to translate Swahili from a Kenyan website.

GPT-3

One of the recent and biggest development in NLP, including the popular media was GPT-3, which was a huge new model that was released by OpenAI. Its exciting as it has started to look the first step on the path to universal models, where we can train an extremely large model on the world knowledge of human languages, of how to do tasks. So we are no longer building a model to detect spam, to detect foreign language content, rather just building all these separate supervised classifiers for every different task, since we have a model that understands.

It is really good at predicting words. The two examples are explained below.

1. Write about Elon Musk in the style of Doctor Seuss

2. Question prediction from a sentence using couple of examples. The model started predicting the questions after just two examples.

The way it generates more text is by just predicting one word at a time, following words to complete its text.

Another Example: Translating human language sentences into SQL.

What is language and its meaning?`

How do we represent the meaning of a word? - Webster’s dictionary definition is really focused on the “word idea”, which is pretty close to the most common way that linguists think about meaning. However, denotational semantics captures word meaning as being a pairing between a word which is a signifier or symbol, and the thing that it signifies, the signified thing which is an idea or thing.

So the meaning of the word chair is the set of things that are chairs. A term that’s also used and similarly applied for the semantics of programming languages. So traditionally the way that meaning has normally been handled in natural language processing systems is to make use of resources like dictionary, and thesaurus in particular. For example, WordNet, which organized words and terms into both synonyms sets of words that can mean the same thing, and hypernyms which correspond to IS-A relationships.

Problem with WordNet

In WordNet, “proficient”” is listed as a synonym for “good”, which is accurate only in some contexts. it is limited as a human constructed thesaurus. Its difficult to keep it up to date, including more current terminology. For example, “wicked”” is there for the wicked witch, but not for more modern colloquial uses. “Ninja” is another example where WordNet is not kept up to date. So it requires a lot of human labor, but even then, it has a set of synonyms but does not really have a good sense of words that means something similar. So this idea of meaning similarity is something that would be really useful to make progress on, and where deep learning models excel.

Problem with traditional NLP

Problem with traditional NLP is that words are regarded as discrete symbols. Symbols like hotel, conference, motel are words, which in deep learning are referred as a localized representation. Because in a statistical machine learning systems, these symbols need to be represented in a statistical model to build a logistic regression model with words as features, typically like an one-hot encoded vector.

One hot encoding vector

One hot encoding vector has a dimension for each different word. So that means that we need huge vectors corresponding to the number of words in our vocabulary. For a high school English dictionary it probably have about 250,000 words in it and probably need a 500,000 dimensional vector to be able to cope with that. But the bigger with discrete symbols is that there is no notion of word relationships and similarity. So for example, if a user searches for Seattle motel, it should match on documents containing Seattle “hotel” as well. So in a mathematical sense, these two vectors are orthogonal, that there’s no natural notion of similarity between them.

Word Embeddings

you shall know a word by the company it keeps. - J. R Firth

Modern deep learning method allows encoding similarity in real value vector themselves. distributional semantics - where word’s meaning is going to be given by the words that frequently appear close to it. This represent a sense for words, meaning as a notion of what context that appears in has been a very successful idea. It proves to be an extremely computational sense of semantics, which has just led to it being used everywhere very successfully in deep learning systems. So when a word appears in a text, it has a context which are a set of words that appear along with it.

Example - “banking”

The word “banking”” occurs in text, and the nearby words (context words) in some sense represent the meaning of the word banking. Based on looking at the words that occur in context as vectors, we want to build dense real valued vector for each word, that in some sense represents the meaning of that word. The way it will represent the meaning of that word, is when this vector would be useful for predicting other words that occur in the context.

A simple 8-dimensional illustration (in reality, usually 300 dimensional vectors are used), of the neural word representations or “word embeddings”, represents the distributed representation, not a localized representation because the meaning of the word banking is spread over all 300 dimensions of the vector. These are called word embeddings because, in a group of words, these representations place them in a high dimensional vector space, and so they’re embedded into that space.

Introduction to word2vec

Word2Vec was introduced by Tomas Mikolov and colleagues in 2013 as a framework for learning word vectors, It uses a lot of text, commonly refer to as a corpus (originated from the Latin word for body), meaning a body of text., with. a vocabulary size of 400,000 and then create vectors for every word. To determine the best vector for each word, we can learn these word vectors from just a big pile of text by doing this distributional similarity task of being able to predict, what words occur in the context of other words. So specifically, going through the texts, and using a center word C, and context words O, calculate the probability of a context word occurring, given the center word according to our current model. Since the corpus is available, it is known that certain words actually occur in the context of that center word, we can keep adjusting the word vectors to maximize the probability that’s assigned to words that actually occur in the context of the center word as we proceed through these texts.

.

Determining the probability of a word occurring in the context of a given center word

For each position in the corpus, we want to predict context words within a window of fixed size, given the center word W_j

Ideally we need to give high probability to words that actually occur in the context. i.e., identify the likelihood of predicting words in the context of other words correctly and this likelihood will be defined in terms of the word vectors. These form the parameters of our model, and it will the product of using each word as the center word, and each other context word in the window to determine the probability of predicting that context word in the center word. And to learn this model, there would be an objective function, also called a cost or a loss that we want to optimize. And essentially maximize the likelihood of the context we see around center words.

Following changes are made to the objective function:

1. Use log likelihood to convert all the products into sums.

2. Also use average log likelihood, denoted by 1/T

3. Minimize our objective function, J(θ) becomes maximizing our predictive accuracy.

Note: Each word will have two word vectors - One word vector for when it’s used as the center word, and a different word vector when that’s used as a context word. This is done to simplify the math and the optimization and makes building word vectors a lot easier,

Likelihood Probability Calculation

For a particular center word v_c and a particular context word u_o, look up the vector representation of each word, and take the dot product of those two vectors.

Dot product is a natural measure for similarity between words because it generates a component that adds to that dot product sum. If both are negative, it’ll add a lot to the dot product sum. If one’s positive and one’s negative,it’ll subtract from the similarity measure. Both of them are zero, won’t change the similarity.

if two words have a larger dot product, that means they’re more similar.

Softmax function

The next step is to convert this how to turn this into a probability distribution and to avoid negative probabilities exponentiate them and normalize by dividing by the sum of the numerator quantity for each different word in the vocabulary. This ensures that the distribution is between 0 and 1. This formulates the softmax function which will take any R in vector and turn it into values between 0 to 1.

1. “max” term - accentuates and emphasizes the big contents in the different dimensions of calculating similarity, as it exponentiates the probabilities.

2. “soft” term - gives a probability distribution of the next possible words.

max function returns just one the biggest term, whereas softmax takes a set of numbers, scales them, and returns a probability distribution.

Construct word vectors

The plan is to optimize the word vectors to minimize the loss function, i.e. maximize the probability of the words that were actually in the context of the center word. θ represents all of the model parameters in one very long vector. So for the model, word vectors are the only parameters. So for each word there are two vectors, context vector and center vector. And each of those is a D dimensional vector, where D might be 300 and we have V many words in the vocabulary. So the model is of size 2 * D * V . So for a vocabulary of size 500k and with a 300 dimensionality vector, there would be millions of millions of parameters, to train and maximize the prediction of context words.

Multivariate Calculus

Derivatives can be computed using multivariate calculus and the gradients can be determined by walking downhill to minimize loss, using stochastic gradient descent. We have J(θ) that is needed to minimize the average negative log likelihood. And then we iterate through the words in each context, to compute J(θ) between M words on both sides except with itself. Then determine the log probability of the context word at that position, given the word that’s in the center position t.

Probability P(o|c) can be determined as the softmax of the dot product of u₀ * V_c normalized by the sum of all probabilities of the word distribution. To compute the gradient, the partial derivative of this expression with respect to every parameter in the model is computed, and all the parameters in the model are the components depending on the dimensions of the word vectors of every word.

Walking through these in steps, the partial derivative with respect to the center word vector(a 300 dimensional word vector) is calculated. Considering the expression as A/B, using log turns it into log A minus log B. Then the partial derivative of V_c is simply u₀

Now using the chain rule the denominator can be computed. This part is essentially going from outside to inside in terms of derivatives. The above image is more cleaner explanation.

Combining all the expressions together, rewriting the expression, by moving the sum w = 1 to v inside the summation expression we end up getting exactly the softmax formula probability that we saw when we started. So the expression more conveniently becomes U₀ minus the sum over X = 1 to V of the probability of X given C times U_x.

And so what we have at that moment is this thing here is an expectation.

This is not an average over all the context vectors weighted by their probability according to the model.it’s always the case with these softmax style models, we get the observed minus the expected for the derivatives. So the model is good if on average it predicts exactly the word vector that we actually see.

The next step is to try and adjust the parameters of our model to try and make the probability estimates as high as we possibly can using stochastic gradient.

Gensim

GENESIM is a package often used for word vectors, it’s not really used for deep learning and for testing glove word vectors were used by loading a hundred dimensional word vectors.

Checking the first 10 dimensions of the word vectors for bread and croissant, these two words are a bit similar, so both of them are negative in the first dimension, positive in the second, negative in the third, positive in the fourth, negative in the fifth and so on. So they might have a fair bit of dot product which is kind of what we want because bread and croissant are kind of similar. Few more examples,

1. Similar to banana

2. Similar to brioche

3. Similar to USA

.

Analogy task

The idea of the analogy task defines that we start with a word like king, and should be able to subtract out a male component from that, add back in a woman component, and then we should be able to ask for the appropriate word, which should be the word queen.

Few other examples are illustrated below using Gensim

.

Even linguistic analogies, such as the analogy of tall is to tallest as long is to longest.

Why two different vectors

Recall the equation for J(θ) taking a sum over every word which is appearing as the center word, and then inside that there’s a second sum which is for each word in the context, where we count each word as a context word, and then for one particular term of that objective function you’ve got a particular context word and a particular center word that you’re then sort of summing over different context words for each center word, and then you’re summing over all of the decisions of different center words. In case the window contains the same word as the center and context word, it messes with the derivatives. while taking them as separate vectors ensures that this issue does not occur. The two vectors would be very similar, but not identical due to technical reasons such as occurring at the ends of documents and other similar differences.

The usual method (followed for word2vec algorithm) is to average those two vectors and consider the average vector as the representation of the word.

Question: How about words with multiple meanings (Homonyms) and common words

1. For a word like star, that can be astronomical object or it can be a movie star,. Taking all those uses of the word star and collapsing them together into one word vector. actually turns out to work rather well.

2. For very common words that are commonly referred to as function words by linguists, which includes words like so and not, prepositions, words such as to, on etc., the suspicion is that the word vectors would not work very well because they occur in all kinds of different contexts. However large language models do a great job in those words as well

Conclusion

Another feature of the word2vec model is that it actually ignores the position of words, ie., it will predict every word around the center word before or after, one or two positions away in either direction using the one probability function. But this sort of destroys the ability at capturing the subtleties more common grammatical words which occur or do not occur at the end of a sentence. But we can build slightly different models that are more sensitive to the structure of sentences, which can then perform better on these errors. So word2vec is more of a framework for building word vectors, and there are several variant precise algorithms within the framework. One such variant is the prediction of either the context words (skip grand model) or the center word.

So to learn word vectors we start off by having a vector for each word type both for context and outside and those vectors we initialize randomly, so that we just place small little numbers that are randomly generated in each vector component. And that’s just the starting point, And from there on we are using an iterative algorithm where we are progressively updating those word vectors, so they do a better job at predicting which words appear in the context of other words. And the way that we are going to do that is by using the gradients and once we have a gradient, we can walk in the opposite direction of the gradient and we are then walking downhill, i.e. we are minimizing your loss and repeat until our word vectors get as good as possible.

Suggested reading

1. Efficient Estimation of Word Representations in Vector Space (original word2vec paper)
2. Distributed Representations of Words and Phrases and their Compositionality (negative sampling paper)

References

1. Video
2. Slides
3. Notes